Analysis of flow in pipes

WELCOME TO THE WORLD OF FLUID MECHANIC

BIODATA PELAJAR

NAMA : LEE CHU FOO

NO MATRIK : AF140176

NO KAD PENGENALAN : 940623-07-5819

ALAMAT SEMASA :J2-03 A , KOLEJ KEDIAMAN PERWIRA, UTHM.

ALAMAT KAMPUNG : 2284, JALAN KULIM, 1400 BUKIT MERTAJAM

EMEL : leechufoo@gmail.com

NO TELEFON: 017-5422696

NAMA RAKAN : WONG CHUNG KAI

NO TELEFON RAKAN : 014-6813688

MOTTO HIDUP : RAJIN ADALAH KEJAYAAN

IDOLA : FACEBOOK CEO MARK ZUCKERBERG

NAME	CHIN ZAN WEN
MATRIC NO.	AF140175
I/C	940623-06-5725
CURRENT ADDRESS	B2-02 KOLEJ KEDIAMAN PEWIRA, UNIVERSITI TUN HUSSEIN ONN MALAYSIA, 86400, PARIT RAJA, BATU PAHAT, JOHOR.
ADDRESS	64. TAMAN SENTOSA, 28300 TRIANG PAHANG.
EMAIL	zanwen_623@hotmail.com
PHONE NO.	017-2958623

NAMA : TAN XIN WANG

NO MATRIK : AF140174

NO KAD PENGENALAN : 940620-01-5845

ALAMAT SEMASA :J2-03 A , KOLEJ KEDIAMAN PERWIRA, TUHM.

ALAMAT KAMPUNG : 60,PEKAN SANGLANG 82100 PONTIAN JOHOR

EMEL : xinwang0620@hotmail.com

NO TELEFON: 017-7600663

NAMA RAKAN : LEE CHU FOO

NO TELEFON RAKAN : 017-5422696

MOTTO HIDUP : USAHA TANGGA KERJAYAAN

IDOLA : BILL GATES

Student’s Name:	Jackie Ting Zhi Keong
Matrix Number:	AF140173
Identity Card Number:	940611-13-5693
Current Address:	Kolej Kediaman Perwira
Email:	jackie7767@hotmail.com
Phone number:	016-8620953

NAMA : BRYAN LEE CHEN SEONG

NO.MATRIKS : AF140191

NO I/C : 940921045431

ALAMAT SEMASA : KOLEJ KEDIAMAN PERWIRA

ALAMAT KAMPUNG : 42, JALAN KOTA LAKSAMANA,2/1

TAMAN KOTA LAKSAMANA, SEK2

75200 MELAKA.

EMEL : rex940921@ymail.com

NO.TELEFON : 010-8980326

NAMA KAWAN : YAU LEONG WEI

NO.TELEFON : 0169724186

MOTTO HIDUP : Tidak ada masalah yang tidak bisa diselesaikan selama ada komitmen bersama untuk menyelesaikannya

IDOLA : David Beck ham

INTRODUCTION

Internal flows through pipes, elbows, tees, valves, etc, as in this oil refinery, are found in nearly every industry.

Osborne Reynolds was the first scientist who had distinguished the type of flow by using a simple apparatus in 1883.

Figure 1: Laminar, Transitional and Turbulent Flows.

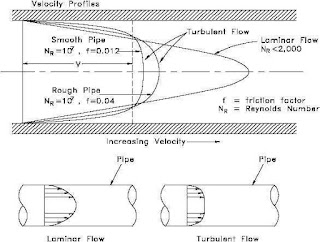
Figure 2: Velocity Profiles of Laminar and Turbulent Flows.

Table 1: Properties of Laminar, Transitional and Turbulent Flows.

Reynolds Number, Re

In fluid mechanics, the Reynolds number (Re) is a dimensionless quantity that is used to help predict similar flow patterns in different fluid flow situations. The concept was introduced by George Gabriel Stokes in 1851,but the Reynolds number is named after Osborne Reynolds (1842–1912), who popularized its use in 1883.

· Introduced by George Gabriel Stokes in 1951

· To predict the pattern of fluid flow

· Ratio inertial forces: Viscous forces

· Flow becomes turbulent is called the Critical Reynolds Number

where:

is the mean velocity of the object relative to the fluid (SI units: m/s)

is a characteristic linear dimension, (m)

is the dynamic viscosity of the fluid (Pa·s or N·s/m² or kg/(m·s))

is the kinematic viscosity(m²/s)

is the density of the fluid (kg/m³).

Table 2: Precise Values of Reynolds Numbers

Example

In a refinery, oil (s.g=0.85 ,v=0.000018 ) flows through a 100 mm

Diameter pipe at 0.50. Determine the Reynolds Number? Is the flow

Laminar or turbulent?

V===0.0637m/s

R===354

R2000 the flow is laminar

Laminar & Turbulent Flow

Figure 3: Laminar & Turbulent Flow

Figure 4: Velocity Profile of Laminar & Turbulent Flow

Question

SAE oil flows in cast iron pipe with flow rate 5.625 L/s and 150mm diameter pipe. Based on Reynolds Number, the flow is laminar or turbulent?
(μ=8.14 x 10-2 Pa.s, Ƿ=869kg/m3)

To determine whether the flow is laminar or turbulent, we need to find R

Ƿ=869kg/m3

Q=5.625L/s

D=150mm

μ=8.14x10-2 Pa.s

V= ?

500ms-1

8x105

Re is more than 4000, therefore, the flow is turbulent flow.

Friction in Pipe

Energy Head Loss,

Major Head Loss,Hf

n Friction occur along the pipe.

Minor Head Loss,Hm

n Friction occur when there is a flow disruption along the pipe (entrance).

Figure : Head loss along a pipe with difference diameters

Factors that affect head loss

A) Flow rate

B) Diameter of the pipe

C) Roughness of the pipe wall

D) Corrosion and scale deposits

E) Viscosity of liquid

F) Length of pipe

G) Fittings

H) Straightness of pipe

In pipe flows the losses due to friction are of two kinds: skin-friction and form friction. The former is due to the roughness of the inner part of the pipe where the fluid comes in

contact with the pipe material, while the latter is due to obstructions present in the line of flow--perhaps a bend, control valve, or anything that changes the course of motion of the flowing fluid.

Friction in Circular Conduits

Friction in non-circular Conduits

Hagen-Poiseuille equation for Laminar flow

-Equation shows that in Laminar flow, the loss of head is proportional to the first power of velocity.

-In Laminar, the friction is independent of the roughness of the pipe but depends on viscosity and density.

Friction factor,f

Friction loss is the loss of energy or “head” that occurs in pipe flow due to viscous effects generated by

the surface of the pipe.Friction Loss is considered as a "major loss" and it is not to be confused with “minor loss”,

which includes energy lost due to obstructions. In mechanical systems such as internal combustion engines,

it refers to the power lost overcoming the friction between two moving surfaces.

This energy drop is dependent on the wall shear stress (τ) between the fluid and pipe surface.

The shear stress of a flow is also dependent on whether the flow is turbulent orlaminar.

For turbulent flow, the pressure drop is dependent on the roughness of the surface.

In laminar flow, the roughness effects of the wall are negligible because, in turbulent flow,

a thin viscous layer is formed near the pipe surface that causes a loss in energy,

while in laminar flow, this viscous layer is non-existent.

Friction factor in laminar flow indicating that the friction factor is proportional to viscosity and

inversely proportional to the velocity, pipe diameter, and fluid density under laminar flow conditions.

The friction factor is independent of pipe roughness in laminar flow because the disturbances caused by

surface roughness are quickly damped by viscosity.

Friction factor in turbulent flow

In turbulent flow, relative roughness contributes a significant part besides Reynolds Number.

Friction factor can be calculated by:

Table: To calculate friction factor

Darcy-Weisbach

Indicating that the friction factor is proportional to viscocity and inversely proportional to the velocity, pipe diameter,

and fluid density under Laminar flow conditions. The friction factor is independent of pipe roughness in Laminar flow

because the disturbances caused by surface roughness are quickly damped by viscosity.

Bernoulli Equation

The Bernoulli Equation is an approximate relation between pressure, velocity, and elevation, and is valid in regions of steady, incompressible

flow where net frictional forces are negligible. It can be considered to be a statement of the conservation of energy principle appropriate for

flowing fluids. The qualitative behavior that is usually labeled with the term "Bernoulli effect" is the lowering of fluid pressure in regions where

the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you

consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy.

The derivation of Bernoulli Equation

An element of fluid, as that in the figure above, has potential energy due to its height, Z above a datum and kinetic energy

due to its velocity, v.If the element has weight, mg then

l potential energy =mgh

l potential energy per unit weight =m/pa{p=density of liquid}

l kinetic energy =1/2 [mv^2]

l kinetic energy per unit weight =[v^2]/2g

At any cross-section the pressure generates a force, the fluid will flow, moving the cross-section, so work will be done. If the pressure at cross section AB is P and the area of the cross-section is a then

lforce on AB =Pa

When the mass, mg of fluid has passed AB, cross-section AB will have moved to A'B'

lvolume passing AB =mg/pg=m/p {p=density of liquid}

Therefore

ldistance AA' =m/pa{p=density of liquid}

lwork done = force distance AA' =Pa x m/pa = Pm/p{p=density of liquid}

lwork done per unit weight =P/pg{p=density of liquid}

This term is know as the pressure energy of the flowing stream.

Summing all of these energy terms gives

As all of these elements of the equation have units of length, they are often referred to as the following:

lPressure head =P/pg {p=density of liquid}

lVelocity head = [v^2]/2g

lPotential head =Z

lTotal head =H

By the principle of conservation of energy the total energy in the system does not change, Thus the total head does not change. So the Bernoulli equation can be written

CONSTANT

As stated above, the Bernoulli equation applies to conditions along a streamline. We can apply it between two points, 1 and 2,

on the streamline in the figure below

Two points joined by a streamline

Total energy per unit weight at 1 = Total energy per unit weight at 2

Total head at 1 = Total head at 2

Practice Worksheet

Problem 1

Water is flowing in a fire hose with a velocity of 1.0 m/s and a pressure of 200000 Pa. At the nozzle the pressure decreases to atmospheric pressure (101300 Pa),

there is no change in height. Use the Bernoulli equation to calculate the velocity of the water exiting the nozzle. (Hint: The density of water is 1000 kg/m3 and

gravity g is 9.8 m/s2 . Pay attention to units!)

Answer:

Since the height does not change (Z1=Z2), the height term can be subtracted from both sides.

Algebraically rearrange the equation to solve for v2, and insert the numbers.

Problem 2

Through a refinery, fuel ethanol is flowing in a pipe at a velocity of 1 m/s and a pressure of 101300 Pa. The refinery needs the ethanol to be at a pressure of 2 atm (202600 Pa) on a lower level.

How far must the pipe drop in height in order to achieve this pressure? Assume the velocity does not change. (Hint: Use the Bernoulli equation. The density of ethanol is 789 kg/m3 and gravity

g is 9.8 m/s2. Pay attention to units!)

Answer:

Since the velocity does not change (v1=v2), the velocity term can be subtracted from both sides.

Rearrange algebraically to solve for change in height.

Moody Chart

Pipe Problem

Pipe problems can be classified into four categories. There categories are based on the type of unknowns that is to be solved.

The Moody chart can be used to solve any problem involving friction losses in long pipe flows. Many such problems involve

considerable iteration and repeated calculations using the chart because the standard Moody chart is essentially a head loss chart.

Generally, types 1 and 2 can be solved directly, where as types 2and 3 require simple trial and error.

The friction factor relates six parameters of the flow:

1. Pipe diameter, D

2. Average velocity, v

3. Fluid density, p

4. Fluid viscosity, v

5. Pipe roughness, e

6. Frictional head losses, hf

Therefore, given any five of these, we can use the friction-factor charts to find

the sixth. Most often, instead of being interested in average velocity, we are interested

in volumetric flow rate, Q .

The four most common types of problems are the following:

Practice Worksheet

Problem 1

Water flows in cast iron pipe with 300mm diameter and 300m length in velocity of 1600m/s. Calculate the friction head loss if

m2/s. (Hint: value of absolute roughness of cast iron is 0.25mm)

Answer:

Given L, Q, and D, then find hf, so it is type 1 problem.

First, find he relative roughness of cast iron pipe,

Second, find the Reynolds Number,

Re>4000 (turbulent)

From Moody Chart,

using E= 0.0008 and Re=4.25 x 10^5 --> f=0.0049

Final, find the friction head loss, hf

Problem 2

A galvanized iron pipe with diameter of 2.54m is used to flow water in horizontal axis at rate 50m3/s.

If the difference heads is 2m and v is given as 1.13 x 10^-6 m2/s, determine the length of the pipe.

(Hint: value of absolute roughness of galvanized iron is 0.15mm)

Answer:

Given hf, Q, and D, then find L, so it is type 2 problem.

First, find he relative roughness of cast iron pipe,

Second, find the Reynolds Number,

Re>4000 (turbulent)

From Moody Chart,

using E=0.00006 and Re=2.2 x 10^7.--->f=0.0112

Find the friction head loss, hf by using energy equation,

Final, find the length of the pipe, L

Problem 3

A 250mm diameter and 100m length of cast iron pipe was use to flow oil ad cause

4m of energy head loss,. If v= 1.0 x 10^-5 m2/s, determine the flow rate of oil in the pipe.

(Hint: value of absolute roughness of cast iron is 0.25mm)

Answer:

Given L, hf, and D, then find Q, so it is type 3 problem.

First, find he relative roughness of cast iron pipe,

Second, find the equation of velocity, v

By using the v value from the above , find the equation of Reynolds Number,

From Moody Chart,

First trial, = 0.02

using E=0.001 and Re= 7.83 x 10^4, ---> f=0.023 not equal to f (trial)

second trial=0.023,

using E= 0.001 and Re=7.3 x 10^4, ---> f=0.023=f (trial)

The value of f(2nd trial)=f (new), the two values converged. By using f(new)=0.023,

and 2.92 m/s, the Q is calculated.

Problem 4

Determine the suitable diameter of galvanized iron pipe in flowing 100 l/s of water at length 250m with 10m of fluid friction. (Hint: value of absolute roughness of galvanized iron is 0.15mm)

Answer:

Given L, hf, and Q, then find D, so it is type 4 problem.

First, find he relative roughness of cast iron pipe,